1. 문제

2. 풀이
a는 0이 아닌 정수이다.
1) a > 0

2) a < 0

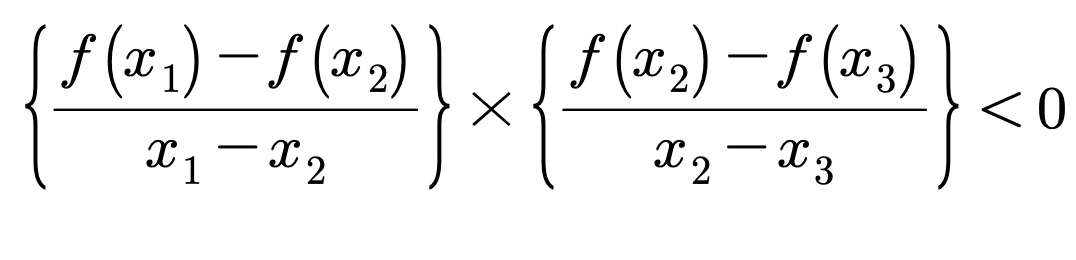
주어진 f(x)가 실수 전체 구간에서 미분 가능한 함수이므로 평균값 정리에 의해
k < x1 < c1 < x2 < c2 < x3 < k + 3/2 를 만족하는 c1, c2에 의해

를 만족시킨다.
열린구간 (k , k + 3/2) 에서 기울기 부호의 변화가 일어나야 하므로
k < 극점 < k + 3/2를 만족하는 k값들의 곱이 -12라는 뜻이다.
a는 0이 아닌 정수이므로, 0에서는 반드시 극점을 가진다.
따라서, k = -1일때
-1 < 0 < 0.5 이므로 위 조건에 만족한다.
정수 k값들의 곱이 -12이고, f(x)가 3차 함수이므로 0이아닌 극값은 단 하나 존재한다.
정수들의 곱으로 나타낼 수 있는 경우의수는 아래 세가지이다.
1) 3, 4
2) -4, -3
3) 12
1) k = 3, 4일때
4 < 극점 < 4.5를 만족 시켜야 한다.
3a / 4에서 극점을 가지므로
3 < a < 27/8이다.
이를 만족시키는 정수는 없다.
2) k = -4, -3일때
-3 < 극점 < 2.5를 만족시켜야 한다.
3a / 4에서 극점을 가지므로
-9/4 < a < -15/8이다.
이를 만족시키는 a는 -2이다.
3) k = 12일때
12 < 극점 < 13.5를 만족시켜야 한다.
3a / 4에서 극점을 가지므로
9 < a < 81/8
a는 10일때 가능하지만, 이때 k = 13일때도 가능하므로 안된다.
2)만 유일하게 가능해 a = -2이다.

정답은 380이다.
사용 기술
정수 분할, 평균값 정리
